One caveat with the binary and multi-class logistic regression is that it only able to classify the data if the data is linearly separable:
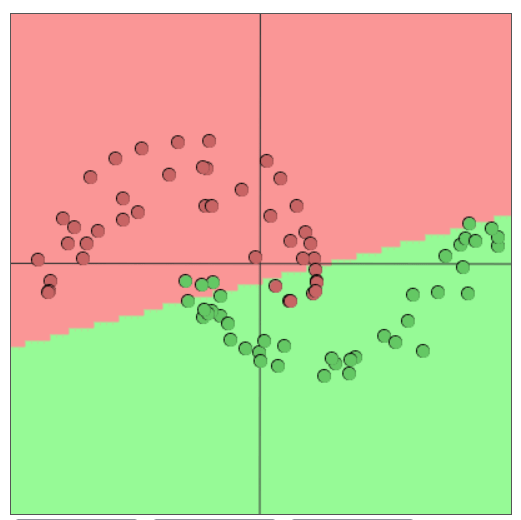
If the data points are non-linearly separable, binary/multi-class logistic regression will only be able to find the best linear line or hyperplane to separate the data points, which is suboptimal solution (some data points is wrongly classified). In binary/multi-class logistic regression we first do a linear transform of the data points, and then classify the data by respectively using a sigmoid function or a softmax function. The problem is both these create linear decision boundary in the original feature space/manifold.
The multi-class logistic regression only operates in linear feature space, so it is easier understand that it only creates linear decision boundaries. However, the binary logistic regression does use the sigmoid function which is a non-linear activation function. The non-linear activation function does warp/bend the linearly transformed feature space:
The neural network structure that mimics binary logistic regression is:

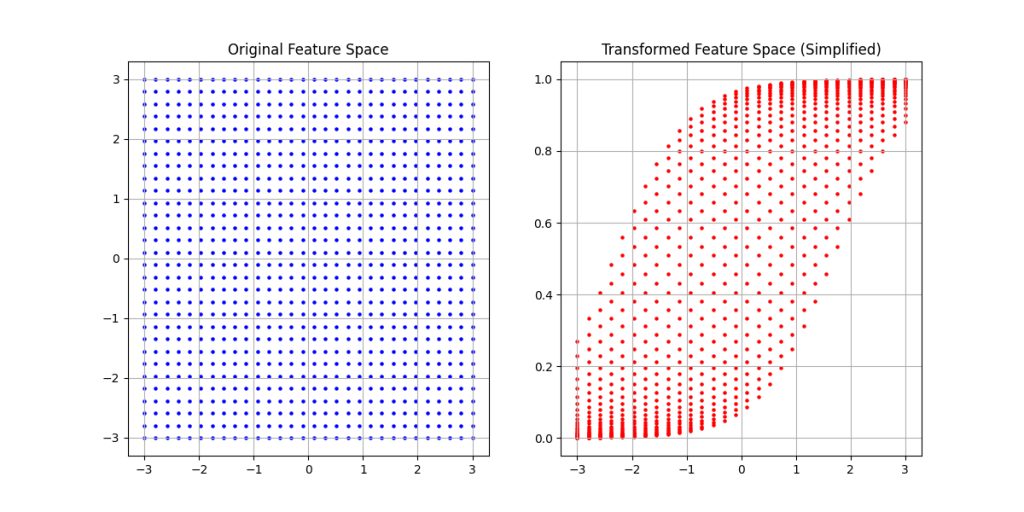
The data points and the decision boundary found after training the neural net, could in the transformed feature space (linear transformation + sigmoid transformation) look like this:
But, the decision boundary is found in a non-linear feature space, so the decision boundary is surely non-linear, right? Well it is not, because if we plot the decision boundary in the original feature space we see it is linear:
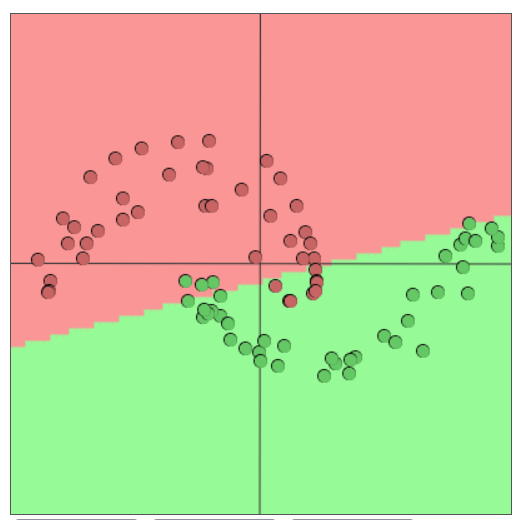
The reason for this is that the sigmoid function only “compresses” the linearly transformed feature space to have a range between 0 and 1, and in such a way that the decision boundary stays linear in the original feature space. The same is true for the tanh activation function which compresses the range to -1 to 1, but it generally is not the case for other non-linear activation functions like ReLU.
So how can this be solved? Well it can be solved by linearly transforming the space, which efficiently edits the already non-linear space into a new non-linear space. This transformation changes the position of the data points so that the scaling effect of the sigmoid activation function and the modified non-linear spaces opens up the possibility for creating decision boundary that is non-linear in original space. Applying a soft max on the logits given by the linear transformation acts as a linear classifier, however you could use any linear classifier (e.g. Support Vector Machines (SVM), linear discriminant analysis (LDA) or logistic regression) on the fully transformed data points. The network is now structured like this:

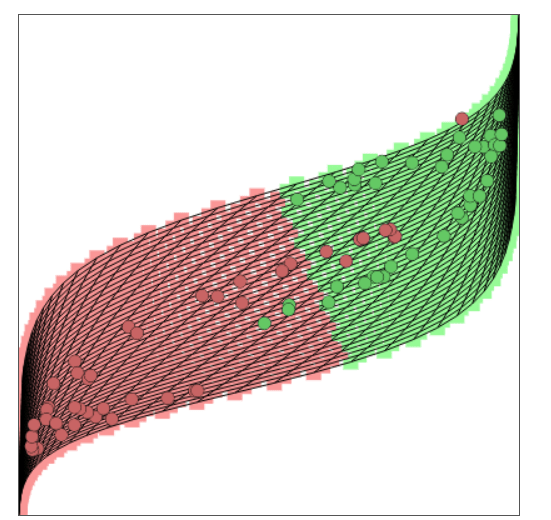
After training the model the final decision boundary could look something like this in the original feature space and the fully transformed feature space (meaning the space after soft max is applied):
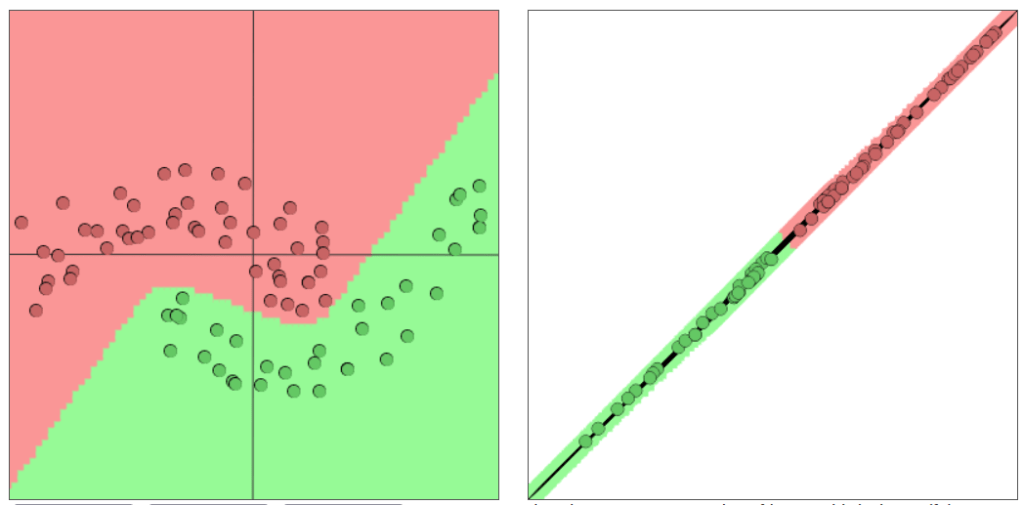
As we can see the decision boundary is non linear in the original feature space and linear in the fully transformed feature space.
(This great tool by Andrej Karpathy is used to create visualization of the transformed spaces.)